知名数据库收录:维普网、万方数据库、龙源期刊网
主管:政协四川省委员会办公厅

主管单位:政协四川省委员会办公厅
主办单位:四川省科教兴川促进会
编辑出版:《科学与财富》杂志社
国内刊号:CN 51-1627/N
国际刊号:ISSN 1671-2226
邮发代号:62-151
出版周期:旬刊
出版地:四川省成都市
发行范围:国内外公开发行
摘要:数学建模是真实世界与数学世界的沟通桥梁。将建模过程与教学内容有机结合,能够有效地促进深度学习。小学数学教学中,经历建模过程包括在现实中寻找建模原型、提出数学问题、通过多层次的表达建立模型、回归生活应用模型等基本环节。
关键词:数学建模;深度学习;小学数学教学
中图分类号:G623.5 文献标志码:A 文章编号:1673-9094(2020)07B-0101-03
荷兰教育家弗赖登塔尔认为,学生学习数学的唯一方法是“再创造”。小学教学中的“建模”过程,实际就是“再创造”的过程。经历建模过程即指学生亲身经历探索和发现数学的过程,它不仅包括寻求问题解决的结果,更强调经历问题产生、分析、解决的过程。从教学角度看,数学建模是一种数学活动,能够有效促进深入学习;从方法论看,深度学习可以通过经历数学建模过程得以开展。
基于此,笔者尝试将数学建模与教学内容有机结合,创设现实的情境,激发学生的建模需求。在多次优化的过程中,经历对比、归纳、简化、概括,把知识建构的主动权交给学生,让学生去尝试、探索、沉淀、总结、内化,完成知识结构的组织。
一、创设现实情境,寻找建模原型
呈现在学生面前的数学模型情境,应该是具有现实意义的,是实际生活中需要用数学知识解决的问题。教学时应从教材的视角出发,联系学生的生活实际整体解读,利用生活中的建模原型,找准建模的知识起点。
在“确定位置”的教学中,教师将生活中的游戏素材及时引入课堂,将未经简化抽象的现实问题与教材的内容有机结合,以游戏的方式呈现。教学由游戏简单地导人:一位学生当船长,发出位置指令;一位学生当炮手,根据指令对隐匿在渔船中的海盗船开炮。游戏中小平面海域内的击炮定位即确定位置的现实原型。这样的情境不是数学化的“已知”和“求證”模式,而是一种真实的需求,是以克服困难为标志的数学问题原型。
二、依托教学情境,提出数学问题
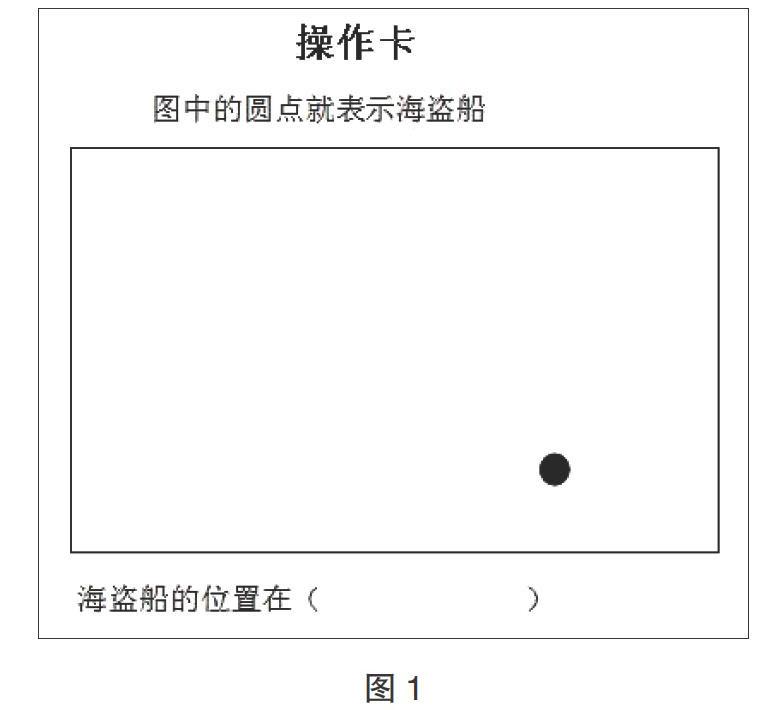
数学问题的产生源于数学情境。从静态角度看,它是学生对定位需求的文字或言语的表达;从动态角度看,它是学生产生问题意识和生成数学思考的过程。根据建模原型,笔者尝试设计了如下的教学情境:由两位学生在配合下,定位击沉海盗船。在海域图顶点、在海域图边上依次出现海盗船后,船长与炮手均能描述并定位。当海域图的中央某处再次出现海盗船时,小船长无法准确描述位置,小炮手无法击沉。(图1)
学生在情境的引导下,产生了值得思考的数学问题:如果将这片海平面看作一个长方形,将海盗船看作一个点,如何在平面中清楚地表达这个点的位置?这样的数学问题不是教师提出的,也不是教材提出的,而是学生用数学的眼光观察世界后提出的疑惑与思考。
三、经历建模过程,建立数学表达
《义务教育数学课程标准(2011年版)》指出,学生学习应当是一个生动活泼的、主动的和富有个性的过程。数学学习是学生个体“生活经验”与群体“履历经验”的叠加与重组,因此在教学中,应充分发挥学生的积极性,鼓励学生自主探究,交流思考,分享发现,获得感悟。
1.个体的表达
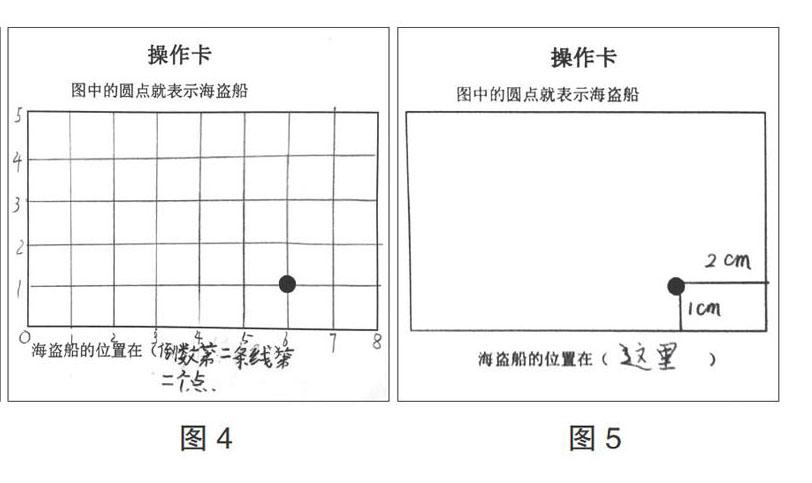
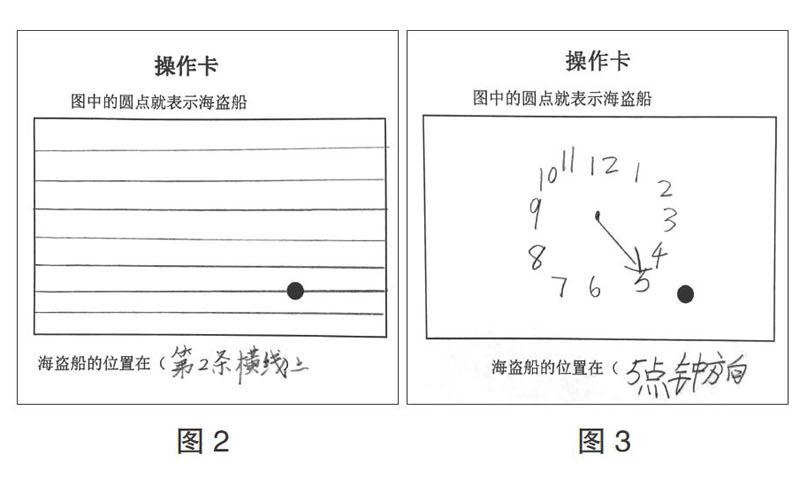
学习中被放在首位的应该是独立思考习惯的培养与思维品质的锤炼,而不是获取特定的知识。因此教学中,教师应为学生提供自主探索的机会,鼓励学生积极思考,使他们从被动的学习者转化为主动的探索者。教学中,教师给予学生独立思考、个性表达的机会,请学生结合操作卡用自己的方法表示出海盗船的位置。(图2、图3、图4、图5)
根据操作活动,教师发现学生能够根据已有的生活经验和知识经验,创造出了许多他们自己的表述方法:东南西北的方位表述法、分成大块区域的描述法、结合钟面的描述法、只画横线的一维描述法、格子图中的二维描述法。这些个体的表达既反映了学生的已有知识经验,也为进一步建构模型提供了宝贵的素材。
2.学生社群的表达
在实际教学中,教师组织学生之间展开交流与讨论,通过分析与评价他人的策略与意图,在反思和碰撞中初步形成模型的雏形。交流中,学生社群一方面需要阅读他人的表征图文并理解他人的想法,另一方面又必须以书面或口头的形式评述他人的模型,在表达个体思维与反思他人观点的同时,达到修正模型与深入思考的双重功效。
在教学活动中,通过学生展示钟面图、一维图、二维图,由学习者、教师和学习伙伴等形成学习社群,通过对话、沟通的方式,提出不同看法以刺激个体反省思考。在交互质疑辩论的过程中,学生发现了最后两种方法是类似的,位置的描述明确而清晰,有的学生建议把行和列标上序号,从零数起。在集体的交流碰撞中,学生逐渐优化确定位置的二维模型表达。
3.数学的表达
在建立模型的过程中,学生不仅需要思考方向正确,还需要自觉努力寻求指向目标的最便捷的逻辑途径,体现思维的和谐进化,进而通过不断重组和转换认识问题中的关系及本质,完善模型结构。因此教学中教师要给学生提供运用符号的机会,让学生经历从“感性”到“理性”,再到“运用”的过程,甚至让学生经历创造符号、完善符号的过程。
运用建模思想观照数学教学,其意义就是要在认知过程中建立一种符号化的、具有数学结构特征的“模型”载体。通过这样具有“模型”功能的载体,为学生提供数学抽象的机会,为后续学习提供基础支撑。结合教学内容,教师在教学中加人了“海盗船来袭,快速记录定位”的环节。由快速记录的需求,学生产生了简化数对写法的需求。在快速记录位置的过程中,学生创造了很多记录的方法,有的学生只写行和列的数字,有的在行和列之间加上了短横,有的在数字之前加上了方向箭头。在不同的写法中,通过观察、对比、交流、求同,学生发现行和列的数字必须规定先后次序,也不能写得连在一起,于是学生就自然生成了数对的数学表达方式——先列再行,中间用逗号分隔,每一个位置外面加上括号。通过解决问题的过程中产生的关于模型表达的多重体验,学生加深了对知识的理解和内化。
四、应用数学模型,回归生活现场
数学模型来源于生活,也运用于生活。数学模型的建模不是一个线性过程,而是一个微调循环的过程。教学中,教师除了引导学生探究模型,更应不断地带领学生从数学世界返回真实世界,即学会用数学的视角去观察世界,用数学的方法认识世界,甚至用数学的思想去改造世界。学生在真实的世界中寻找原型,应用模型,建构对数学模型的表象支撑。
在教学中,教师出示了三幅数学情境图,通过逐一出示人物小军的座位、动物小猴家的位置、小熊做操的位置,引导学生观察描述。在对比求同中,学生发现这三幅场景表面看起来不一样,但如果用数学的眼光来观察,都可以用数对(3,2)来表示。学生的思维豁然开朗,头脑中模型也更加丰富多样。学生体会了模型的实际应用价值,思维走向了深刻。
用所建立的数学模型来解答生活中的数学问题,有助于学生体会数学模型的实际应有价值,体验到所学知识的用途和益处,有助于建立数学与生活之间的联系,即用数学的眼光来观察,用数学的模型来解释。
综上所述,结合教材内容,从现实生活中找到建模原型,依托原型提出数学问题,通过师生之间的相互启发,经历建模过程,建立数学表达,将问题的解决与生活实际相联结沟通,是数学学习的有效方式。从个体表达到数学表达,从不全面到全面,从生活到数学、又回归生活,既是一段数学建模的经历,也是一个深入学习的过程。
责任编辑:丁伟红
收稿日期:2019-12-17
作者简介:沈君,江阴市花园实验小学(江苏江阴,214431)教师。