知名数据库收录:维普网、万方数据库、龙源期刊网
主管:政协四川省委员会办公厅

主管单位:政协四川省委员会办公厅
主办单位:四川省科教兴川促进会
编辑出版:《科学与财富》杂志社
国内刊号:CN 51-1627/N
国际刊号:ISSN 1671-2226
邮发代号:62-151
出版周期:旬刊
出版地:四川省成都市
发行范围:国内外公开发行
陈凯

请想象这样的场景:一只出门远行的兔子面对着许多条岔路,这些道路的状态可用宽敞程度、明亮程度、平坦程度这三种属性来进行描述,所以说,其中有些道路是宽敞的,有些是狭窄的;有些道路是明亮的,有些是幽暗的;有些道路是平坦的,有些是崎岖的。兔子随身携带着“指路神器”,会显示出推荐的路线——假设是根据众多兔子前辈经验归纳而来的结果:那些同时具有宽敞、明亮、崎岖属性的道路,或同时具有宽敞、幽暗、崎岖属性的道路,或同时具有狭窄、明亮、平坦属性的道路,都是值得优先选取的。尽管兔子选择道路的场景是虚拟的,其选择原因也不必深究(如宽敞、明亮、平坦的道路暗藏有陷阱),但对于复杂现象经由分离和提纯抽取出关键要素,再由建立系统模型来实现预测,这样的思维过程是无时无刻不真实发生在人类头脑中的。实际上,模型是人类理解世界的重要工具,那些与客观现实具有相似结构的模型,在科学方法上称为同构模型(与此相对应的还有虚构模型),同构模型被用于模仿、刻画、代表目标对象,所谓同构,是指作为模型的系统,和作为研究对象的系统,两个系统中每一部分以及各部分之间的互动关系,在对方都能找到对应物或对应的事件。无论是虚拟的兔子选择道路的场景,还是真实的生活中进行某种选择的场景,只要是以抽象推理的方式来进行预测和决策,那么预测和决策的过程就都能够映射到某个同构的模型。基于以上原因,笔者很乐于将仿佛童话故事的虚拟场景,看成是已更换为相对纯净叙事事件的准真实情境,并将之用于自己的教学。
兔子的“指路神器”是一个装置,但要实现这个装置,首先需要的是一个模型,如果将故事中提炼出的属性编码成二进制数值,就可以有很多种办法来构造模型。然而,需求细节上的不同,导致选择模型的不同,从而会使得最终成品之间有着巨大的差别。这里就体现出基于虚拟场景开展教学的一个优势,它首先将学习者的经验从真实环境中暂时剥离出来,然后从需求出发亲自构筑模型,并将模型作为拟真的桥梁,去对照和“重新”发现客观现实中所存在着的不同的侧面,若不是模型的存在,这些多姿多彩的观测面极有可能隐遁于日常平凡的生活语境之中而被视作理所当然。
● 逻辑运算模型
仔细对照已经完成的所谓“指路神器”的功能,可以直接将需求中的输入和输出的二进制数值的逻辑关系推理出来。所谓“同时具有”,可看作逻辑中的与运算,而三种可以分别选择的情况,其实就对应着将三个与运算的结果再进行逻辑中的或运算,如果用Python语言写下来,那么语句是这样的:
print(a and b and(not c) or a and (not b) and (not c) or (not a) and b and c)
这样就可以根据逻辑运算,将实物的数字逻辑电路图画出来,然而,语句中出现的12种逻辑运算对应了12个逻辑门,真的需要那样复杂吗?用数学模型就可以揭示出简化的方法,构造数学模型的方法不止一种,常用的有卡诺图模型,但这里用到的是更直观的3D散点图(如http://grapher.mathpix.com),可以将道路属性的逻辑值转化为数字,True用3表示(用1也可以,但用3看起来更清楚),False用0表示,这样的话,宽敞、明亮、崎岖即可表示为坐标点(3,3,0),其他两个点则分别是(3,0,0)和(0,3,3)。因为散点图工具可以旋转,所以就能更清晰地判断三个点之间的关系。从图1可以明显看出,(3,3,0)和(3,0,0)这两个点处于两个垂直平面的交线上,其意义是,这两点位置的不同,仅仅是因为明亮与否这一指标上有所变化,所以,只要道路是既宽敞又崎岖,就不用管明亮指标上的变化而直接得出此道路可通行的结论了。
这样就可以将先前的Python代码修改为:
print(a and not c or(not a) and b and c)
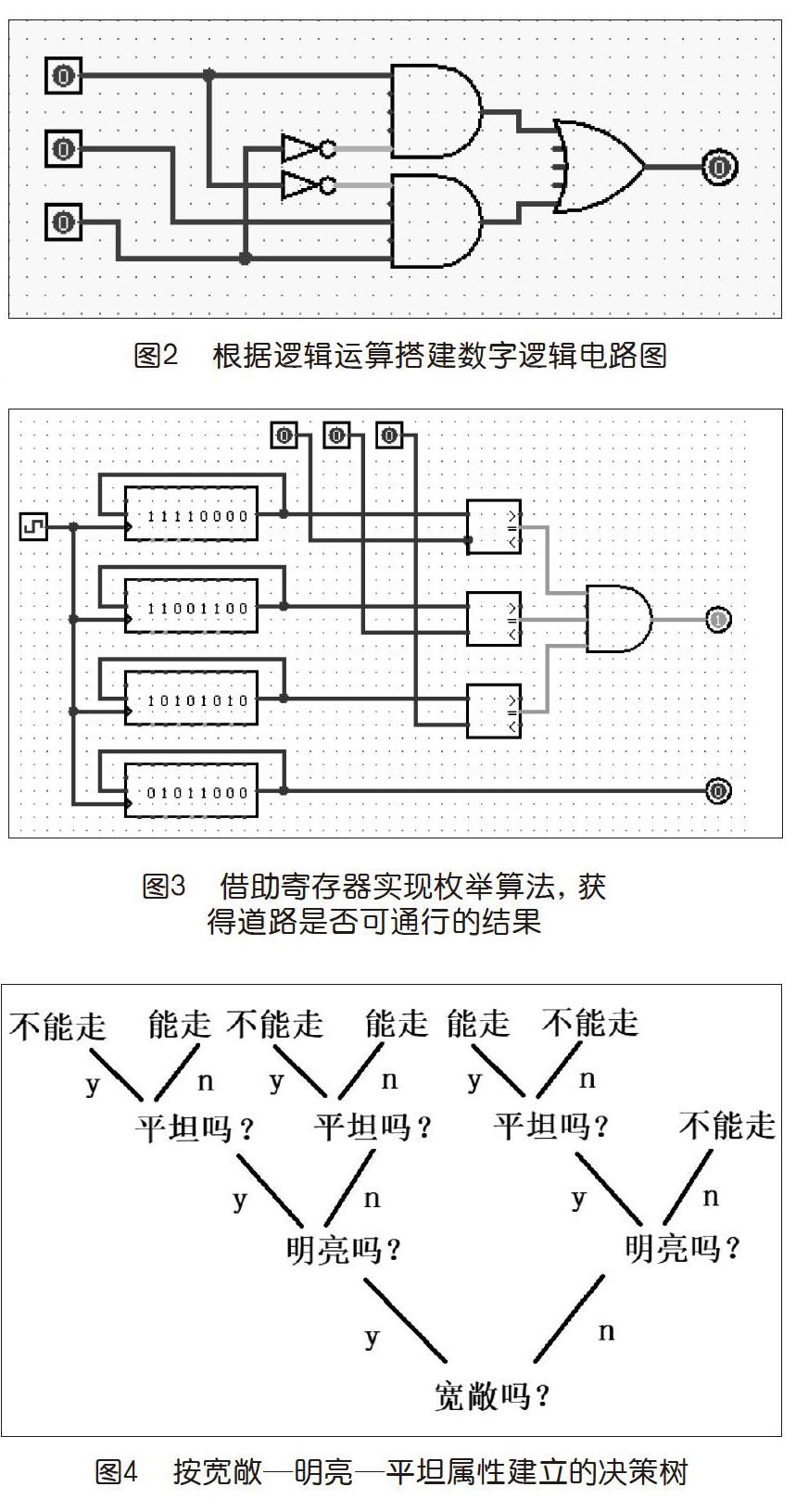
根据以上逻辑运算公式搭建起数字逻辑电路也十分容易,如图2所示。
三种属性的逻辑值之间的关系很容易用3D散点图直观显现出来,但四种属性或更多属性的逻辑值,却无法与现实中的几何立体图形相对应,因为人的头脑缺少对高维度空间关系的把握能力,只能通过计算机模拟,将高维度中发生的事件映射到低维度空间中来加以理解,这就更加凸显了计算机建模对补充和增强人脑能力的重要性。
● 枚举算法模型
若仔细分析需求,会想到上述装置存在的一个问题,由于输入和输出的关系被做死到了数字逻辑电路中,所以就无法轻易改变其用途了。在日常应用中,往往希望一个装置具有存储信息的能力,那么就可以根据不同的情况,将不同的信息预先存储到装置中。对于兔子的指路神器来说也是如此,希望能将兔子所遇见的道路属性情况与是否选择这条道路的结果存于寄存器中,然后输入当前道路状况并获取结果,这个过程实际上和枚举算法实现的过程是一致的,如图3所示。
装置中有四个移位寄存器,前三个代表着道路的三种属性,最下面的一个移位寄存器则代表是否应当选择这条道路。通过点击时钟脉冲获取到所有八种可能性,当与门的输出结果为1时,就可以观察最底下的移位寄存器的输出结果。当然,也可将移位寄存器改为RAM存储器,电路会稍微复杂一些。与先前纯粹的逻辑运算的模型相比,这个枚举算法的模型允许输出结果和输入数据之间,存在多种可能性,也就是说,对于同一组输入数据,也是有可能得到截然相反的结果的,这样似乎更能体现出客观现实的复杂性。
针对不同的需求,这个装置也有较强的可扩展性,如希望一旦匹配到相关属性值,则不再接受新的点击输入,使输出的结果固定下来,这就可以对应另一种常见的算法——顺序查找算法。
● 决策树模型
假设兔子的指路神器是一个基于对话的装置,当面临某条道路时,这个装置会依次针对道路的情况发问,如:“这条道路是宽敞的还是狭窄的?”在得到肯定或否定的回答后,它会接着继续问:“那么这条道路是明亮的还是幽暗的?”……乍一看,这种输入方式不如先前所用的方式便捷,但如果道路的属性非常多,除了文中所提到的几种,还有若干属性,如坡度是否陡峭?食物是否充分?等等,那么,指路神器就应该先从具有较强区分度的属性开始提问,尽快做出决策,在某种特殊的情况下(如兔子身后正有大灰狼追赶),这个需求显得尤其重要。
即便是只有三种属性,如若将提问和回答所产生的决策的分支画在纸上,也可以看出,提问先后顺序影响着决策的效率,如按是否宽敞、是否明亮、是否平坦的顺序,得到的图样如上页图4所示。
如按是否宽敞,是否平坦,是否明亮的顺序提问,得到的图样如图5所示。
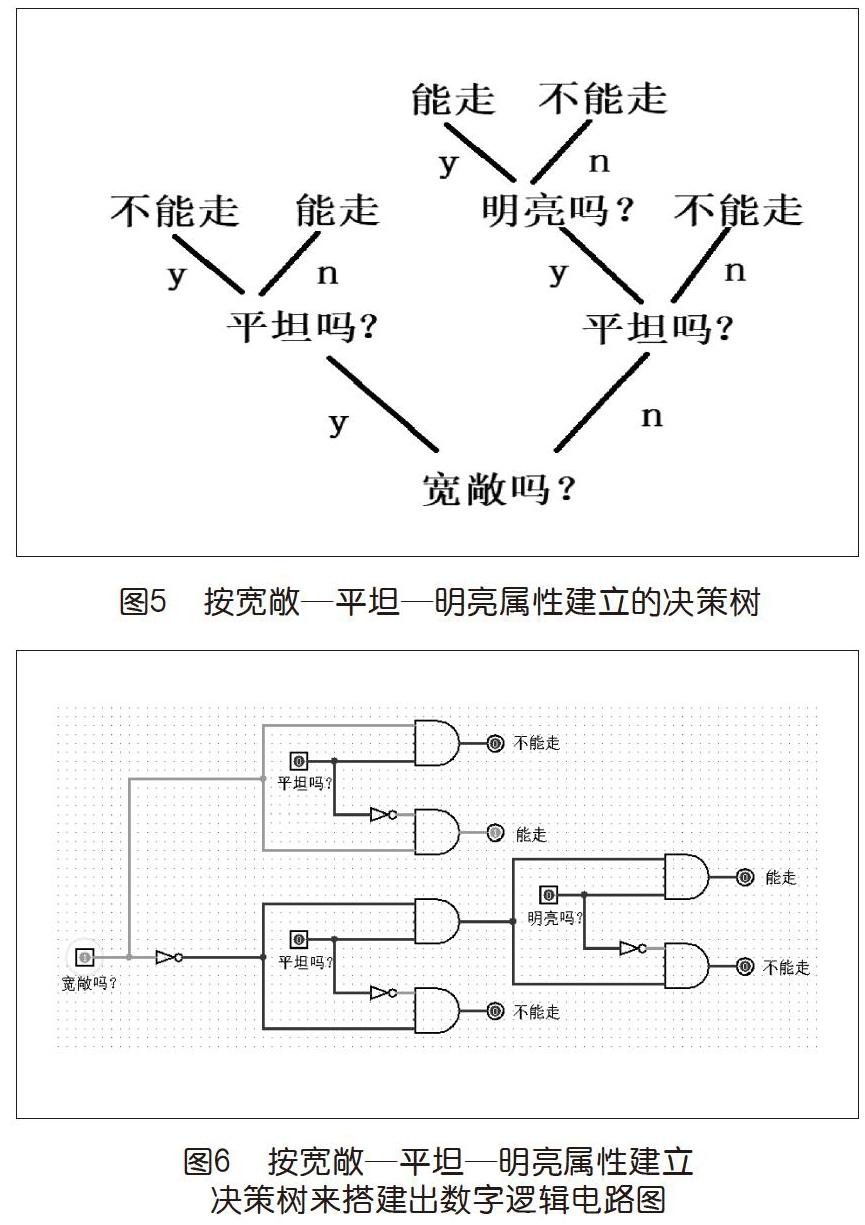
所以,如果按是否宽敞、是否平坦、是否明亮的順序提问,那么,指路神器的数字逻辑电路可能如图6所示。
使用时,按从左到右的顺序依次回答问题,而每次回答的结果,是点亮决策树中的某一路分支,如先回答宽敞,再回答不平坦,则最快两步就可以得到明确的答案。
然而这个装置的设计者,是如何知晓,在询问宽敞与否之后,到底是应该先询问平坦与否,还是明亮与否呢?这个问题便与信息熵和信息增益有了密切的联系,需要借助数学的方法来计算并确定每个决策分支应该判别的属性。这个模型体现出生物在作出决策时,对事物或事件特征的选取,是存在优先级关系的。
另外,这个装置的数字逻辑电路图也有很不一般的特点,它实际上是多个完全相同的结构迭代而成的,像一棵真正的树,具有分形的特征。也就是说,如果要扩充决策树,就只要将同样的结构复制粘贴然后对接到决策树的最终节点上就可以了,或者,也可以反过来操作,先建立一棵分支齐全的决策树,然后根据实际情况对其进行减枝从而简化决策过程。另一个让人惊讶的地方是,如果要改变决策树的功能,根本不需要重新搭建决策树,只要更换一下输入属性和输出结果的标签就可以了。这样的话,就可以借助寄存器,搭建出一个适用于各种情况的“万能”决策树,大家如有兴趣,不妨亲自尝试一下。
本文的例子和信息的编码、计算机系统、逻辑运算、算法等教学内容都有一定的联系,这样就方便教师建立起一个相对统一的情境和具有持续探索空间的实验任务,将日常信息技术教学内容中多个分散的知识和技能整合在一起。