知名数据库收录:维普网、万方数据库、龙源期刊网
主管:政协四川省委员会办公厅

主管单位:政协四川省委员会办公厅
主办单位:四川省科教兴川促进会
编辑出版:《科学与财富》杂志社
国内刊号:CN 51-1627/N
国际刊号:ISSN 1671-2226
邮发代号:62-151
出版周期:旬刊
出版地:四川省成都市
发行范围:国内外公开发行
林赛雅
● 计算思维教育的宗旨
计算思维是一种能够把问题及其解决方案表述成为通过计算工具进行信息处理的形式化思维过程,[1]即个体运用计算机科学的思想方法,在形成解决方案的过程中产生的一系列思维活动,包括发现问题、抽象问题、构造模型,再利用計算机自动化解决同类问题的一系列过程与方法。所以,课堂应当以学生为主体,从实际问题出发,引导他们积极思考,通过问题的抽象、形式化、构造和自动化过程,努力达成“信息技术解决问题方法的掌握、认知思维的发展和人机互动的理解”的培养目标。教师应精心设计课堂活动,努力使内容更加贴近学生的生活与学习,在真实体验与实践中发展学生利用信息技术思考与解决问题的独特能力。
● 基于真实情境的项目式教学让“计算思维”落地
项目式教学是一种基于真实情境的系统性的学习和研究活动。项目式教学最显著的特点是“以项目为主线、教师为引导、学生为主体”,使学生走向综合性学习,走向体验式学习,走向个性化学习。
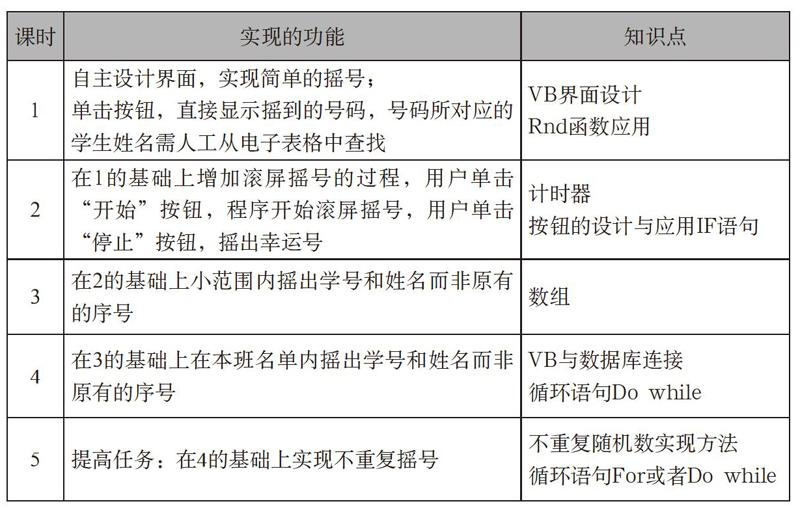
在笔者所在学校的高中通用课堂上,当通用技术教师提问,暂无学生主动发言回答时,教师会用摇号器随机抽取一个学生回答。生活中还有许多地方也会用到随机摇号工具,如班会课中的幸运同学的产生等。所以笔者在算法与VB程序设计单元教学中设置了基于真实情境的“随机摇出本班级同学姓名”的项目活动。“随机摇号”项目式教学方案实施课时安排如下表所示。
第一课时在学生着手设计界面之前,教师不提供参考效果。这种做法旨在让学生更好地体验发现问题、主动思考、着手设计、解决问题的过程。另外,本课时有一个重要环节——编号。教师引导学生思考摇号程序:“摇出的是什么号?”“学号OR序号?”“班级学生学号不连续,摇学号是否恰当?”“若摇序号,你准备如何编写序号?”“各序号对应的又是谁?”教师根据学生的思路逐步引导,学生思考后得出的结论会更深刻,符合项目式学习对学生综合能力培养的特点。学生从Rnd函数总结出特定范围内的随机整数的表达式,初步体现了计算思维的培养。
第二课时教师引导学生从生活经验和自己的想法出发,对第一课时实现的摇号程序找找茬,顺理成章引出计时器控件。该课时看似只是增加了计时器,但学生要正确处理按钮、计时器之间的关系,也并非易事。首先,学生需要厘清:“摇号过程由谁实现?是计时器还是按钮?”“既然是计时器实现,那么按钮是否无用了?”“按钮有用,它的作用又是什么呢?”“开始停止一定需要两个按钮吗?”“若一个按钮如何实现?”此外,学生还需通过调试确定恰到好处的摇号频率,总结计时器Interval属性值设为多少合适。这个过程可以引导学生在用分析问题和用计算机解决问题时要逐步形成适宜计算机处理的问题的解决思路,亦可建立模型或模拟解决方案的意识。
第三、四课时根据学生在第二课时中提出的程序的另一缺点——仅显示序号未显示姓名,引出这两课时程序要改进的方向。第三课时先小范围进行摇号,即将小范围的学生的姓名和学号分别存入两个数组,根据随机序号提取姓名和学号。请学生思考:这样的解决方案有何不足?引导学生发现两个明显的缺点:①学生数量较多的情况下,数组元素赋值麻烦。②程序只能摇出数组中的学生,换一批学生就无法摇出来。从而有了第四课时,从前一课时到后一课时水到渠成,自然过渡,此过程也进一步培养了学生计算思维能力。
第五课时是为分层教学而设计。项目式教学存在的常见问题:大部分学生可以跟上教师设定的教学方案和教学进度,但由于多堂课完成一个完整的项目,有少部分学生渐渐地就掉队了。所以,笔者设置第五课时这样一个提高型的教学任务和目标,有能力者探究实现,其间教师适当引导,更深一步提高学生的计算思维。进度慢的学生则先保证实现基本目标。这样的设计也体现了项目式教学研究性的特点,体现了信息技术学科重视学生全面而又个性化发展的特点。
这样的项目式教学设计,不仅仅为了学习VB语言,更重要的是学生可以完完整整地体验从真实问题出发,到问题分析,再到最后问题解决的整个过程。而此过程中,VB仅仅是实现问题解决的一个合适的工具。学生学会面对复杂问题时,要怎样抽丝剥茧,一步一步分析问题,提取关键数据,建立基本模型,最后再用程序语言实现的完整步骤。
● 结束语
在基于真实问题解决理念的算法与程序学习中,通过对不同实际问题的分析、建模、编程、执行、优化等步骤,学生的计算思维能力能够得到大幅度的提升。但在这个过程中,教师必须从学生学习与生活的实际出发,选择恰当的项目,设计有助于将思维活动更细化展开的活动,在解决问题的过程中,借助计算机等科学工具将人类思维中的输入、编码、储存、加工、输出显性地表现出来[2],让学生在感知与体验中,不断习得解决较为复杂的问题所需要的计算方法,深化计算思维,进而落实计算思维能力的提高。
参考文献:
[1]李锋,王吉庆.计算思维教育:从“为计算”到“用计算”[J].中国电化教育,2015(10):6-10.
[2]龚静,侯长林,张新婷.计算思维能力发展模型与教学程序研究[J].现代教育技术,2018(04):48-54.